Contents

1. Introduction and Code Download


2. What is an Upper Triangular Matrix


3. Upper Triangular Matrix Calculation using Algothingy


4. References

Introduction and Code Download

These matrices are often a step in the process of solving bigger problems in various scientific and engineering fields. If you’re studying or working in areas like computer science, physics, or any engineering discipline, you’ll find that these matrices help simplify many tasks.

In this blog post, you can find production-strength, fully tested, and performant software for converting matrices to upper triangular matrices. As we explore these matrices, we’ll look at how they make it easier to solve systems of linear equations, how they are used in breaking down matrices into simpler forms (like in LU decomposition), and how they help in finding the eigenvalues of a matrix. Finally, if you are also interested in the "dual" concept of lower triangular matrices .

What is an Upper Triangular Matrix

To understand what an upper triangular matrix is let's illustrate this with an example. Imagine that you have a system of three equations and three unknowns \(x, y, z\) as shown below.

The common approach to solving this kind of system is to cast it as a matrix-vector equation and invert the matrix. Inverting such a 3x3 matrix requires different kinds of algorithms, like Gaussian elimination [1]. In general, this is computationally expensive. On the other hand, assume that the coefficients \(a_2\), \(a_3\), and \(b_3\) are zero; in that case, the system of equations would reduce to

Solving this system is straightforward. Starting by solving for \(z\), we get \(z = \frac{d_3}{c_3}\). Then, we move to the middle equation and find that \(y = \frac{d_2 - c_2 z}{b_2}\). With \(z\) and \(y\) known, we finally go to the first equation to solve for \(x\). Interestingly, if some coefficients are zero, then the system of equations can be solved easily without much computational effort. It's also interesting to see what the system of equations looks like in matrix-vector notation, as shown below.

The matrix above is called an upper triangular matrix (in this case, a 3x3 upper triangular matrix). In a nutshell, an upper triangular matrix is a squared matrix whose entries below the diagonal are zero (diagonal might be included) [2].

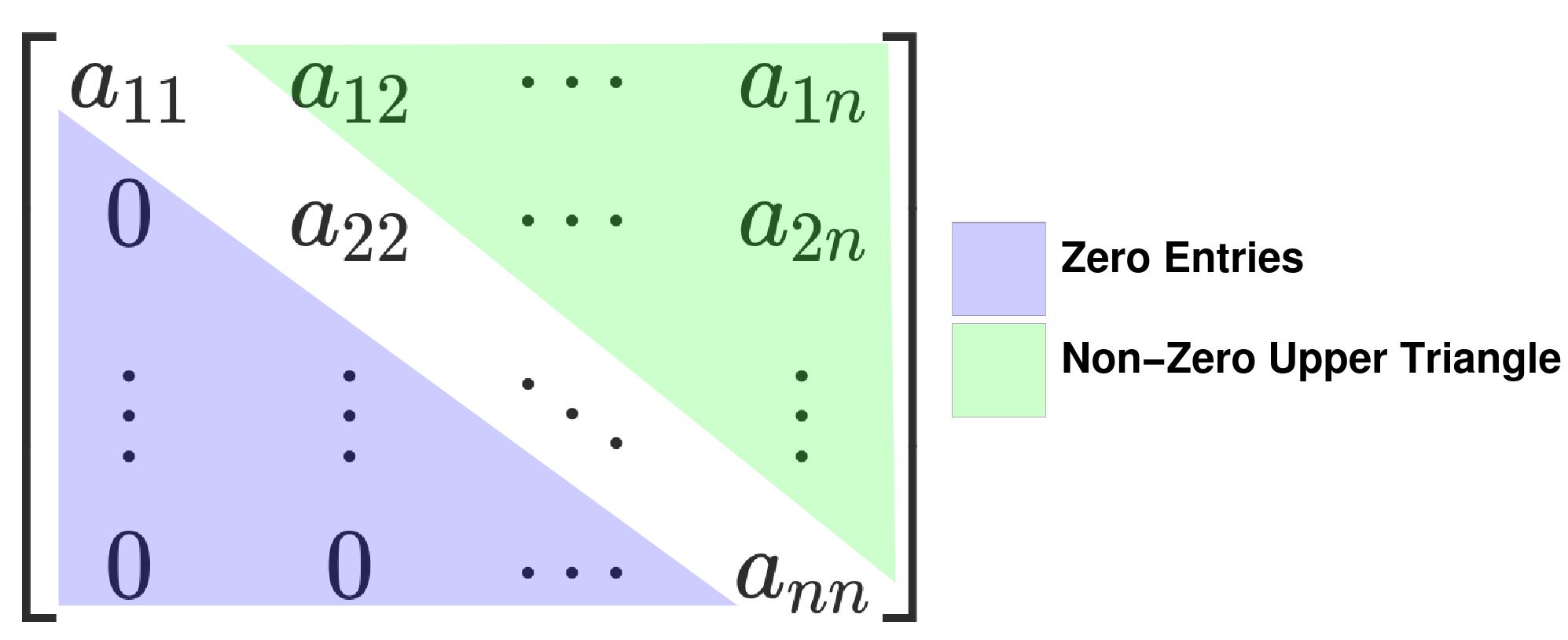
From Figure 1, we see why upper triangular matrices are called upper triangular. This is the upper triangle of the matrix contains the non-zero entries! The diagonal of the matrix, may or may not be all zeroes.
Upper (and lower) triangular matrices have several properties that make some computations a lot easier.

• Matrix Eigenvalues: The eigenvalues of an upper triangular matrix are just the values in its diagonal [3] (Reference [3] is a great resource for anyone wanting to go deeper into advanced topics in Linear Algebra)


• Matrix Determinant: Since, the determinant of a matrix is the product of its eigenvalues [3], then the determinant is the product of the values in its diagonal. That is, if \(A\) is an upper triangular matrix, then \[ det(A) = \prod_{i = 1}^{n} a_{ii} \]


• Solution to Linear Systems: If a linear system can be described with an upper triangular matrix, then back substitution can find the solution to the system.

Upper Triangular Matrix Calculation using Algothingy

Upper triangular matrices can be easily calculated using Algothingy. Below, we show you examples in the available programming languages of how to use Algothingy implementations to make a given matrix upper triangular. We show examples with 2x2 upper triangular matrices and 3x3 upper triangular matrices.

#include <iostream>
#include "implementation.hpp"

int main(){

  /*2x2 example*/
  bool zero_diagonal = false;
  std::vector<std::vector<float>> m = {{1.f, 2.f}, {3.f, 4.f}};

  std::vector<std::vector<float>> upper22 = MakeUpperTriangular(m, zero_diagonal);//upper22 = {{1.f, 2.f}, {0.f, 4.f}}

  /*3x3 example*/
  zero_diagonal = true;
  m = {{1.f, 2.f, 3.f}, {4.f, 5.f, 6.f}, {7.f, 8.f, 9.f}};
  auto upper33 = MakeUpperTriangular(m, zero_diagonal); //upper33 = {{0.f, 2.f, 3.f}, {0.f, 0.f, 6.f}, {0.f, 0.f, 0.f}}


  return 0;
}

References

Disclosure: Please note that some links in this post are affiliate links, and at no additional cost to you, Algothingy will earn a commission if you decide to make a purchase after clicking through the link. We recommend these references because of their quality, and not because of the commission Algothingy will receive from your purchases.

1. Gaussian Elimination


2. Linear Algebra Done Right, Sheldon Axler


3. Advanced Linear Algebra, Steven Roman