Introduction

When we think about understanding shapes and forms through a computer's eyes, circle fitting is a central concept. It's like teaching a machine to play connect-the-dots but with a twist: the machine finds the best possible circle that can go through those dots. This process of fitting cirlces it's a vital part of computer vision and computational geometry, touching everything from scanning your favorite cookies for quality control to helping cars see the road better.

Recognizing circles in images is part of what is called low-level vision [1]. Low-level vision is all about interpreting the raw pixels in an image to identify fundamental features. Think of it as teaching a computer to see the outlines and shapes that make up the visual world, without worrying about what these shapes represent. For example, detecting edges is a key part of understanding the structure of objects within an image. These edges form boundaries that can be used to identify shapes, such as circles, squares, or triangles.

Circle fitting is a specialized task within this realm, focusing on identifying and precisely defining circles within the visual clutter of real-world or artificial images. Being able to accurately detect and fit circles to these features is essential for numerous applications, from gauging sizes in industrial quality control to tracking objects in surveillance footage. Or as in the case study for this publication, finding the size of craters in the moon.

Circles and Some Theory

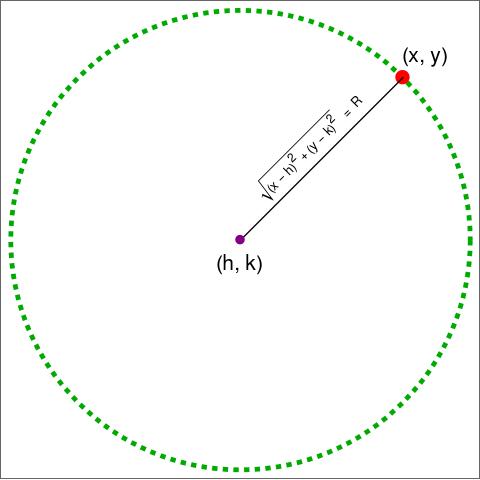
From high school, we learned that a circle is the set of points that are all at the same distance away from a given center, as shown in Figure 1. In this case, all the points on the circle are a distance \(R\) from the point \((h, k)\). A circle with these characteristics satisfies an equation of the form

\[(x - h)^2 + (y - k)^2 = R^2.\]

Expanding the squares and grouping constants and terms with \(x\) and \(y\), the previous equation can be written as

\[x^2-2 h x+y^2-2 k y + h^2+k^2-r^2 = 0.\]

This means that in general a circle centered at \((h, k)\) and radius \(R\), can be written in the form

\[x^2 + y^2 - Ax - By - C = 0,\]

where \(A, B, C\) are constants. Therefore, if we are given a set of points \(\{\{x_1, y_1\}, \ldots, \{x_n, y_n\}\}\) that approximate the shape of a circle, and we want to find the circle that best fits this data, we must find the values of \(A, B, C\) that minimize the equation, making it as close to zero as possible. Formally, if we define \(F(x, y) = x^2 + y^2 - Ax - By - C\), we can then define the loss function:

\[loss(A, B, C) = \frac{1}{2}\sum_{i = 1}^{n} F(x_i, y_i)^2.\]

Finding the parameters \(A, B, C\) that make the \(loss\) function as small as possible is equivalent to doing least squares fit for fitting a circle through the data. Following [2], finding the values that minimize the \(loss\) function is equivalent to solving the system of equations

The matrix in the left-hand side is symmetric, so we can use Cholesky Decomposition to solve the system. Explanation on Cholesky decomposition and software implementation for it can be found here. Finally, we can connect the values of \(A, B, C\) to the center coordinates \((h, k)\) and its radius \(R\) as follows

Let's conclude with a study case of how to use Algothingy to solve a practical problem that can be solved with the help of the function LeastSquaresCircleFit available at the end of this publication.

Case Study Using Algothingy

We are going to calculate the size of one of the most famous craters in the moon, the Tycho crater [3], as shown in Figure 2. To get an approximate measurement of it, we will do the following steps:

• Extract the boundary of the moon from Figure 2.


• Use Algothingy implementation for fitting circles to get the radius of the moon in pixels


• Using the known diameter of the moon, calculate the number of pixels per kilometer in the image


• Measure the diameter of the Tycho crater in pixels.


• Convert the diameter of the crater in pixels to kilometers.

In Figure 3, we see every step in the implementation to get the moon's diameter in pixels. After extracting the points from the moon's boundary (Figure 3, top right) we use Algothingy's implementation LeastSquaresCircleFit in the language available for this implementation as shown in the subsection below.

#include <iostream>

#include "implementation.hpp"


int main(){

    std::vector<Point2D<int>> points = {{202, 382}, ..., {210, 21}};
    LeastSquaresFitResult<Circle> result = LeastSquaresCircleFit(points);
    double radius = result.fittedObject.radius;
    double residuals = result.residuals;

    std::cout<<"Residuals from fit "<<residuals<<" on circle of radius "<<radius<<std::endl;

    return 0;
}

After running Algothingy's implementation for doing circle fit, we found that the diameter of the moon is 362 pixels (Figure 3 bottom right). A quick search on Wikipedia shows that the moon's diameter is 3475 kilometers. This means that the resolution of the image is given by

This means that each pixel represents approximately 9.6 kilometers. Measuring the Tycho Crater in Figure 2, we find that it is between 8 and 9 pixels, meaning we estimate the diameter (\(\phi\)) of the crater to be between

A quick Wikipedia search reveals that the estimated diameter of the crater is 85 kilometers. This value falls within our estimation. Not bad at all!

References

Disclosure: Please note that some links in this post are affiliate links, and at no additional cost to you, Algothingy will earn a commission if you decide to make a purchase after clicking through the link. We recommend these references because of their quality, and not because of the commission Algothingy will receive from your purchases.

1. Nixon et al. Feature Extraction & Image Processing for Computer Vision, 4th ed.


2. Nguyen, H.H., Desbenoit, B. and Daniel, M. (2014), Realistic road path reconstruction from GIS data. Computer Graphics Forum, 33: 259-268


3. Wood, 21st Century Atlas of the Moon